摄像机/观察空间
要定义一个摄像机,我们需要它在世界空间中的位置、观察的方向、一个指向它右侧的向量以及一个指向它上方的向量。细心的读者可能已经注意到我们实际上创建了一个三个单位轴相互垂直的、以摄像机的位置为原点的坐标系。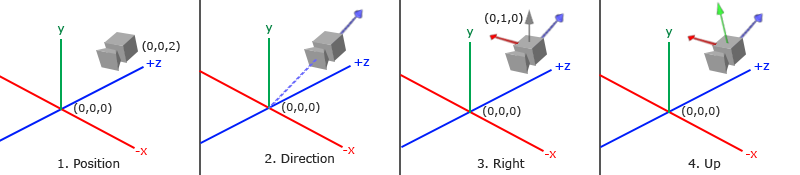
1. 摄像机位置
获取摄像机位置很简单。摄像机位置简单来说就是世界空间中一个指向摄像机位置的向量。我们把摄像机位置设置为上一节中的那个相同的位置:
glm::vec3 cameraPos = glm::vec3(0.0f, 0.0f, 3.0f);
2. 摄像机方向
下一个需要的向量是摄像机的方向,这里指的是摄像机指向哪个方向。现在我们让摄像机指向场景原点:(0, 0, 0)。还记得如果将两个矢量相减,我们就能得到这两个矢量的差吗?用场景原点向量减去摄像机位置向量的结果就是摄像机的指向向量。由于我们知道摄像机指向z轴负方向,但我们希望方向向量(Direction Vector)指向摄像机的z轴正方向。如果我们交换相减的顺序,我们就会获得一个指向摄像机正z轴方向的向量:
glm::vec3 cameraTarget = glm::vec3(0.0f, 0.0f, 0.0f);
glm::vec3 cameraDirection = glm::normalize(cameraPos - cameraTarget);
3. 右轴
我们需要的另一个向量是一个右向量(Right Vector),它代表摄像机空间的x轴的正方向。为获取右向量我们需要先使用一个小技巧:先定义一个上向量(Up Vector)。接下来把上向量和第二步得到的方向向量进行叉乘。两个向量叉乘的结果会同时垂直于两向量,因此我们会得到指向x轴正方向的那个向量(如果我们交换两个向量叉乘的顺序就会得到相反的指向x轴负方向的向量):
glm::vec3 up = glm::vec3(0.0f, 1.0f, 0.0f);
glm::vec3 cameraRight = glm::normalize(glm::cross(up, cameraDirection));
4. 上轴
现在我们已经有了x轴向量和z轴向量,获取一个指向摄像机的正y轴向量就相对简单了:我们把右向量和方向向量进行叉乘:
glm::vec3 cameraUp = glm::cross(cameraDirection, cameraRight);
在叉乘和一些小技巧的帮助下,我们创建了所有构成观察/摄像机空间的向量。对于想学到更多数学原理的读者,提示一下,在线性代数中这个处理叫做格拉姆—施密特正交化(Gram-Schmidt Process)。使用这些摄像机向量我们就可以创建一个LookAt矩阵了,它在创建摄像机的时候非常有用。
Look At
使用矩阵的好处之一是如果你使用3个相互垂直(或非线性)的轴定义了一个坐标空间,你可以用这3个轴外加一个平移向量来创建一个矩阵,并且你可以用这个矩阵乘以任何向量来将其变换到那个坐标空间。这正是LookAt矩阵所做的,现在我们有了3个相互垂直的轴和一个定义摄像机空间的位置坐标,我们可以创建我们自己的LookAt矩阵了:
$$
LookAt = \begin{bmatrix} \color{red}{R_x} & \color{red}{R_y} & \color{red}{R_z} & 0 \ \color{green}{U_x} & \color{green}{U_y} & \color{green}{U_z} & 0 \ \color{blue}{D_x} & \color{blue}{D_y} & \color{blue}{D_z} & 0 \ 0 & 0 & 0 & 1 \end{bmatrix} * \begin{bmatrix} 1 & 0 & 0 & -\color{purple}{P_x} \ 0 & 1 & 0 & -\color{purple}{P_y} \ 0 & 0 & 1 & -\color{purple}{P_z} \ 0 & 0 & 0 & 1 \end{bmatrix}
$$
glm::mat4 view;
//三个参数分别为 摄像机位置,目标位置,世界坐标上向量
view = glm::lookAt(glm::vec3(0.0f, 0.0f, 3.0f),
glm::vec3(0.0f, 0.0f, 0.0f),
glm::vec3(0.0f, 1.0f, 0.0f));
在这里实现一个Camera类来维护LookAt矩阵
#ifndef CAMERA_H
#define CAMERA_H
#include <glad/glad.h>
#include <glm/glm.hpp>
#include <glm/gtc/matrix_transform.hpp>
#include <glm/gtc/type_ptr.hpp>
#include <string>
#include <iostream>
#include <fstream>
#include <sstream>
class Camera
{
public:
glm::vec3 cameraUp;
glm::vec3 cameraPos;
glm::vec3 cameraFront;
glm::mat4 lookAt;
Camera(glm::vec3 cameraPos, glm::vec3 cameraFront, glm::vec3 cameraUp)
{
this->cameraPos = cameraPos;
this->cameraFront = cameraFront;
this->cameraUp = cameraUp;
this->lookAt = glm::lookAt(cameraPos, cameraPos + cameraFront, cameraUp);
}
void changePos(glm::vec3 cameraPos) {
this->cameraPos = cameraPos;
this->lookAt = glm::lookAt(cameraPos, cameraPos + this->cameraFront, this->cameraUp);
}
void changeFront(glm::vec3 cameraFront) {
this->cameraFront = cameraFront;
this->lookAt = glm::lookAt(cameraPos, cameraPos + this->cameraFront, this->cameraUp);
}
};
#endif // CAMERA_H
自由移动
让摄像机绕着场景转的确很有趣,但是让我们自己移动摄像机会更有趣!首先我们必须设置一个摄像机系统,所以在我们的程序前面定义一些摄像机变量很有用:
glm::vec3 cameraPos = glm::vec3(0.0f, 0.0f, 3.0f);
glm::vec3 cameraFront = glm::vec3(0.0f, 0.0f, -1.0f);
glm::vec3 cameraUp = glm::vec3(0.0f, 1.0f, 0.0f);
LookAt函数现在成了:
view = glm::lookAt(cameraPos, cameraPos + cameraFront, cameraUp);
我们首先将摄像机位置设置为之前定义的cameraPos。方向是当前的位置加上我们刚刚定义的方向向量。这样能保证无论我们怎么移动,摄像机都会注视着目标方向。让我们摆弄一下这些向量,在按下某些按钮时更新cameraPos向量。
我们已经为GLFW的键盘输入定义过一个processInput函数了,我们来新添加几个需要检查的按键命令:
void processInput(GLFWwindow *window)
{
...
float cameraSpeed = 0.05f; // adjust accordingly
if (glfwGetKey(window, GLFW_KEY_W) == GLFW_PRESS)
cameraPos += cameraSpeed * cameraFront;
if (glfwGetKey(window, GLFW_KEY_S) == GLFW_PRESS)
cameraPos -= cameraSpeed * cameraFront;
if (glfwGetKey(window, GLFW_KEY_A) == GLFW_PRESS)
cameraPos -= glm::normalize(glm::cross(cameraFront, cameraUp)) * cameraSpeed;
if (glfwGetKey(window, GLFW_KEY_D) == GLFW_PRESS)
cameraPos += glm::normalize(glm::cross(cameraFront, cameraUp)) * cameraSpeed;
}
当我们按下WASD键的任意一个,摄像机的位置都会相应更新。如果我们希望向前或向后移动,我们就把位置向量加上或减去方向向量。如果我们希望向左右移动,我们使用叉乘来创建一个右向量(Right Vector),并沿着它相应移动就可以了。这样就创建了使用摄像机时熟悉的横移(Strafe)效果。
注意,我们对右向量进行了标准化。如果我们没对这个向量进行标准化,最后的叉乘结果会根据cameraFront变量返回大小不同的向量。如果我们不对向量进行标准化,我们就得根据摄像机的朝向不同加速或减速移动了,但如果进行了标准化移动就是匀速的。
现在你就应该能够移动摄像机了,虽然移动速度和系统有关,你可能会需要调整一下cameraSpeed。
移动速度
目前我们的移动速度是个常量。理论上没什么问题,但是实际情况下根据处理器的能力不同,有些人可能会比其他人每秒绘制更多帧,也就是以更高的频率调用processInput函数。结果就是,根据配置的不同,有些人可能移动很快,而有些人会移动很慢。当你发布你的程序的时候,你必须确保它在所有硬件上移动速度都一样。
图形程序和游戏通常会跟踪一个时间差(Deltatime)变量,它储存了渲染上一帧所用的时间。我们把所有速度都去乘以deltaTime值。结果就是,如果我们的deltaTime很大,就意味着上一帧的渲染花费了更多时间,所以这一帧的速度需要变得更高来平衡渲染所花去的时间。使用这种方法时,无论你的电脑快还是慢,摄像机的速度都会相应平衡,这样每个用户的体验就都一样了。
我们跟踪两个全局变量来计算出deltaTime值:
float deltaTime = 0.0f; // 当前帧与上一帧的时间差
float lastFrame = 0.0f; // 上一帧的时间
在每一帧中我们计算出新的deltaTime以备后用。
float currentFrame = glfwGetTime();
deltaTime = currentFrame - lastFrame;
lastFrame = currentFrame;
现在我们有了deltaTime,在计算速度的时候可以将其考虑进去了:
void processInput(GLFWwindow *window)
{
float cameraSpeed = 2.5f * deltaTime;
...
}
与前面的部分结合在一起,我们有了一个更流畅点的摄像机系统
欧拉角
欧拉角(Euler Angle)是可以表示3D空间中任何旋转的3个值,由莱昂哈德·欧拉(Leonhard Euler)在18世纪提出。一共有3种欧拉角:俯仰角(Pitch)、偏航角(Yaw)和滚转角(Roll),下面的图片展示了它们的含义:
![[Pasted image 20241011112708.png]]
俯仰角是描述我们如何往上或往下看的角,可以在第一张图中看到。第二张图展示了偏航角,偏航角表示我们往左和往右看的程度。滚转角代表我们如何翻滚摄像机,通常在太空飞船的摄像机中使用。每个欧拉角都有一个值来表示,把三个角结合起来我们就能够计算3D空间中任何的旋转向量了。
对于我们的摄像机系统来说,我们只关心俯仰角和偏航角,所以我们不会讨论滚转角。给定一个俯仰角和偏航角,我们可以把它们转换为一个代表新的方向向量的3D向量。俯仰角和偏航角转换为方向向量的处理需要一些三角学知识,我们先从最基本的情况开始:
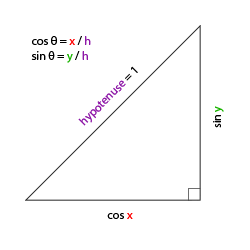
如果我们把斜边边长定义为1,我们就能知道邻边的长度是$$cos x/h=cos x/1=cos xcos x/h=cos x/1=cos x$$它的对边是$$sin y/h=sin y/1=sin ysin y/h=sin y/1=sin y$$这样我们获得了能够得到x和y方向长度的通用公式,它们取决于所给的角度。我们使用它来计算方向向量的分量:
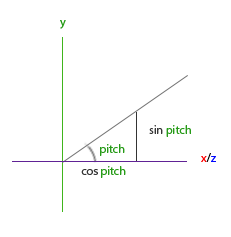
这个三角形看起来和前面的三角形很像,所以如果我们想象自己在xz平面上,看向y轴,我们可以基于第一个三角形计算来计算它的长度/y方向的强度(Strength)(我们往上或往下看多少)。从图中我们可以看到对于一个给定俯仰角的y值等于$$ sin θ $$
direction.y = sin(glm::radians(pitch)); // 注意我们先把角度转为弧度
这里我们只更新了y值,仔细观察x和z分量也被影响了。从三角形中我们可以看到它们的值等于:
direction.x = cos(glm::radians(pitch));
direction.z = cos(glm::radians(pitch));
看看我们是否能够为偏航角找到需要的分量:
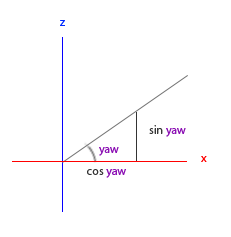
就像俯仰角的三角形一样,我们可以看到x分量取决于cos(yaw)的值,z值同样取决于偏航角的正弦值。把这个加到前面的值中,会得到基于俯仰角和偏航角的方向向量:
direction.x = cos(glm::radians(pitch)) * cos(glm::radians(yaw)); // 译注:direction代表摄像机的前轴(Front),这个前轴是和本文第一幅图片的第二个摄像机的方向向量是相反的
direction.y = sin(glm::radians(pitch));
direction.z = cos(glm::radians(pitch)) * sin(glm::radians(yaw));
