1. 整体方法
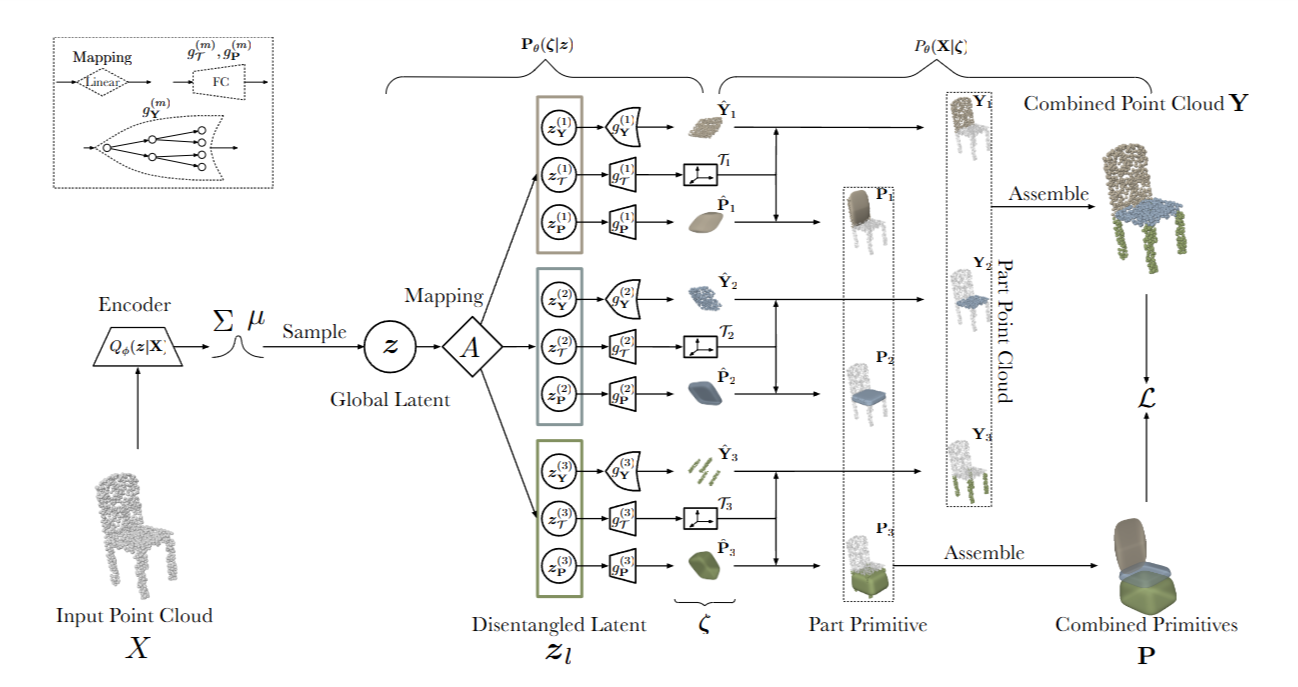
方法以超二次曲线为基元,通过co-segmentation的方法预测基元以及点的归属。
文章将基于部件的点云分割和编辑的任务分为以下三部分:
1、将无标签的点云分割为语义上有意义的部分
2、在通过类型和关系位姿区分每个部分
3、将上述分解的内容用一个隐藏层表示,允许在生成过程中人为地调整其类型和位姿
为了解决这些问题,文章对于输入点云X的m个部分生成了另一个表示部件的点云$Y_m$ ,与一个部件的超二次曲线原型$\hat{P_m}$。为了解决问题2,我们通过一个仿射变换矩阵$T_m$来获取$\hat{P_m}$和$\hat{Y_m}$的标准参考位姿,因此有:$$P_m=T_m(\hat{P_m})\space and\space Y_m=T_m(\hat{Y_m})$$从而表示点云和基元部件的原始位姿。
因此 文章这里使用了边缘似然 即贝叶斯方法去计算在整体latent z分布下 不同交集$ζ_m = { \hat{Y_m}, \hat{P_m}, T_m}$ 的union,$ζ = ⋃^M_{m=1} ζ_m$ ,因此我们定义了训练目标为对输入X针对参数$\theta$的边缘似然$$P_{\theta}(X) = \int P_{\theta}(X,z,ζ)dzdζ$$
对其取对数和Jensen不等式得到:
$$logP_{\theta}(X) = log\int{P_{\theta}(X,z,ζ)dzd}ζ$$$$=log\int\frac{Q_φ(z,\zeta|X)}{Q_φ(z,\zeta|X}P_\theta(X,z,\zeta)dzd\zeta$$
$$\geq\int{Q_φ(z,\zeta|X)log\frac{P_\theta(X,z,\zeta)}{Q_φ(z,\zeta|X)}}dzd\zeta$$
