1、整体方法
超二次曲面参数方程如下所示:$$r(\eta,\omega)=\left[\begin{aligned}a_1cos^{\epsilon1}\eta cos^{\epsilon2}\omega\a_2cos^{\epsilon1}\eta sin^{\epsilon2}\omega\a_3sin^{\epsilon1}\eta\end{aligned}\right]\space\space\begin{aligned}-\pi/2\leq\eta\leq\pi/2\-\pi\leq\omega\leq\pi\end{aligned}$$
其中$a=[a_1,a_2,a_3]$定义了超二次曲面的大小 $\epsilon=[\epsilon_1,\epsilon_2]$定义了超二次曲面的全局形状。根据常识,方法将$\epsilon_1,\epsilon_2$的范围定义在$[0.1,1.9]$之间去避免生成非凸的形状。这样的方程定义了一个基于标准坐标系原点的超二次曲面。为了使其能够处于任意位置,同时定义了一个位移$t=[t_x,t_y,t_z]$向量定义位置,四元组向量$q=[q_0,q_1,q_2,q_3]$定义了旋转。组合在一起定义了仿射变换矩阵为$T(x)=R(\lambda)x+t(\lambda)$
文章的输入基于体素组,因此编码器解码器如下所示: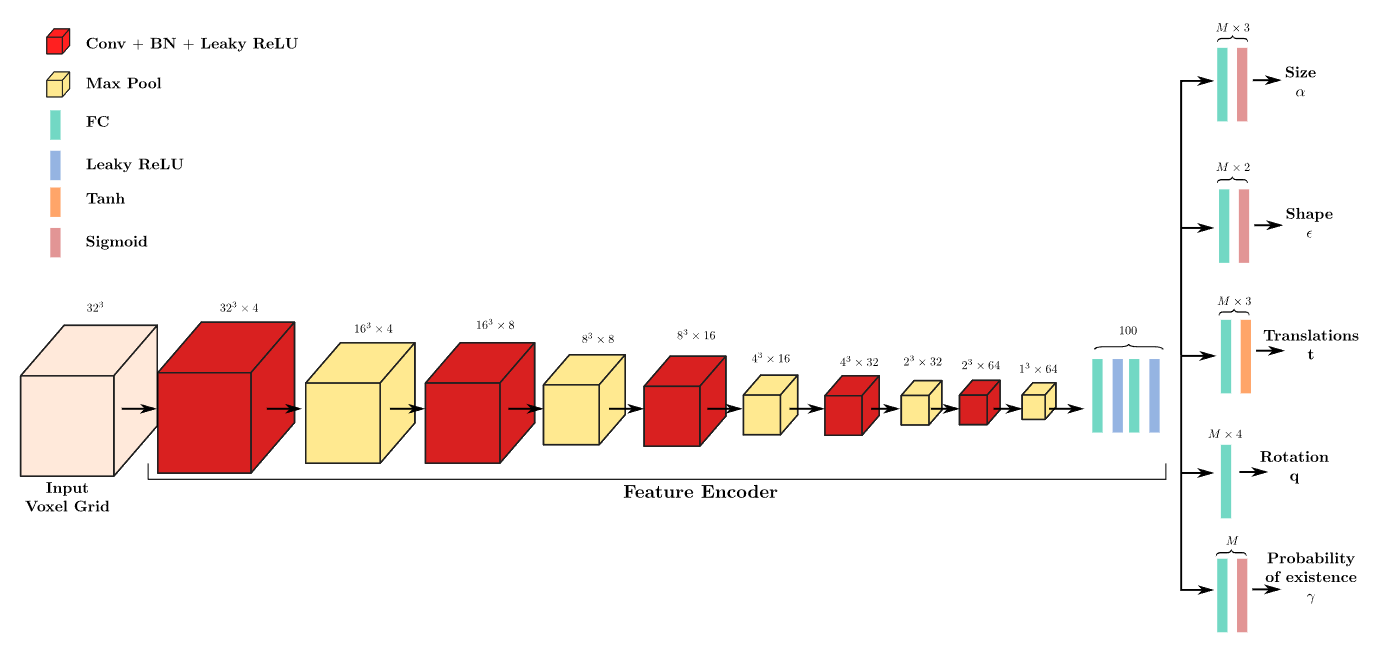
2、重建损失
文章通过与双向SDFloss测试后,使用标准的倒角距离作为重建损失来监督重建效果。即:
$$L_D(P,X)=L_{P->X}(P,X)+L_{X->P}(X,P)$$
其中$P->X$表示预测的基元$P$到原始点云$X$的距离,$X->P$则表示原始点云$X$到预测基元$P$的距离。文章对两组距离加以不同的权重,分别为1.2与0.8。
基元到点云
目标点云由一组3D点组成$X={x_i}^N_{i=1}$。同样,这里将m个基元的连续表面近似为一组点$Y_m={y_k^m}^K_{k=1}$通过这样的离散化表示便能计算基元到目标点云的距离。对于任意一个基元上的任意一点$y_k^m$,我们计算他到目标点云的最近一个点的最近距离,最终取所有点的平均值作为距离$L^m_{P->X}$即:$$L^m_{P->X}(P,X)=\frac{1}{K}\sum^K_{k=1}\Delta^m_k$$
其中$$\Delta^m_k=\min_{i=1,..,N}||T_m(x_i)-y_k^m||2$$
因为并非所有物体都能用固定的N个基元表示,这里同时预测了当前基元存在的概率$p(z_m)$即有$p(z)=\Pi_m(z_m)$。对于所有基元到点云的距离loss就可以表示为:$$L{P->X}(P,X)=E_{p(z)}\left[\sum_{m=1}^ML_{P->X}^m(P,X)\right]$$$$=\sum_{m=1}^M\gamma_mL_{P->X}^m(P,X)$$点云到基元
文章定义了$$\Delta_i^m=\min_{k=1,..,K}||T_m(x_i)-y_k^m||2$$相较于之前基元到点云不同的是,这里需要对K个点根据预测的基元最小化距离。在这里同样需要取每个基元的存在概率$\Delta_i^m$。不同的是,这里需要检索出离点云X中每一个点距离最近且存在的基元$m(z_m=1)$:$$L{X->P}(X,P)=E_{p(z)}\left[\sum_{x_i∈X}\min_{m|z_m=1}\Delta_i^m\right]$$
这里注意到上述方法在基元数量M特别大时,时间复杂度会达到$2^M$的量级,因此十分耗时。文章这里提供了一种线性时间复杂度的计算方法来替代这种复杂的计算。这里假设对于每个基元的存在性$\Delta_i^m$是升序排列的,即:$$\Delta_i^1\leq\Delta_i^2\leq…\leq\Delta_i^M$$在假设这样的序列的情况下,我们可以声明如下:如果第一个基元存在,则第一个基元就是与当前点最接近的基元。如果第一个基元不存在而第二个基元存在,则第二个基元是当前点最近的基元,余下以此类推。$$\min_{m|z_m=1}\Delta_i^m=\left{\begin{align}
&\Delta_i^1,ifz_1=1 \
&\Delta_i^2,ifz_1=0,z_2=1\
&…\
&\Delta_i^M,ifz_m=0,…,z_M=1
\end{align}\right.$$因此可以通过上式简化上上式有:$$L_{X->P}(X,P)=\sum_{x_i∈X}\sum^M_{m=1}\Delta_i^m\gamma_m\prod^{m-1}\bar{m}(1-\gamma{\bar{m}})$$$\Delta_{\bar{m}}$为除了$m$更远的基元的存在概率。
